1.1. TEHNIČKO CRTANJE

Tehnički crteži predstavljaju najvažniji dio tehničke dokumentacije. U različite svrhe njima se koristi velik broj tehničkog osoblja različitog stupnja naobrazbe. Zbog toga oni moraju na jasan jednostavan i razumljiv način jednoznačno definirati prikazani objekt ili sustav.

Pri tome je važna primjena jednoznačno utvrđenih normi i pravila. Propisi kojima se utvrđuju pravila izradbe tehničkih crteža obuhvaćeni su nacionalnim normama npr. DIN (Deutsche Industrie Norm) ili ANSI (American National Standard Institute), a posebice za područje elektrotehnike jedinstvenim međunarodnim normama IEC (Internatinal Electrotechnical Commission).

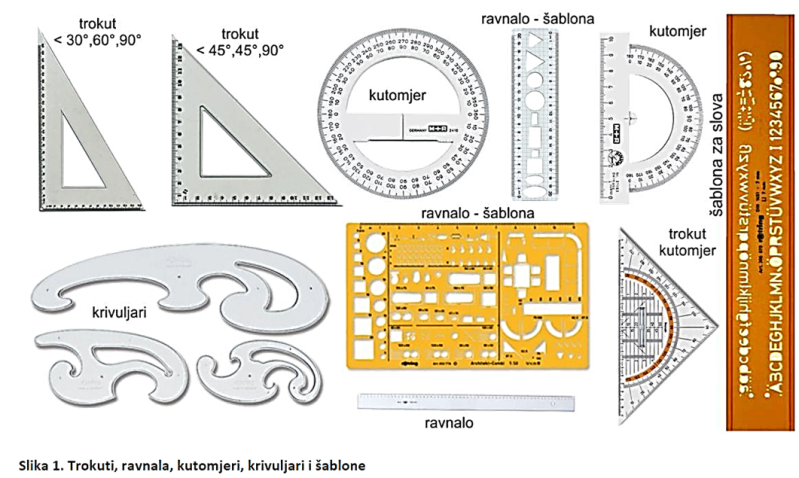
  • Uvod u predmet - pribor za tehničko crtanje

U pribor za tehničko crtanje spada: tehnička olovka, trokuti, ravnala, kutomjeri, krivuljari, šablone i šestari.

Trokuti za tehničko crtanje:

1. Jednakokračni, pravokutni trokut: 45° – 90° – 45°

2. Raznostranični, pravokutni trokut: 60° – 90° – 30°

VAŽNO !

Od ovoga trenutka, nadalje učenici su dužni pod satom imati uredan, osnovni pribor za tehničko crtanje, dakle:

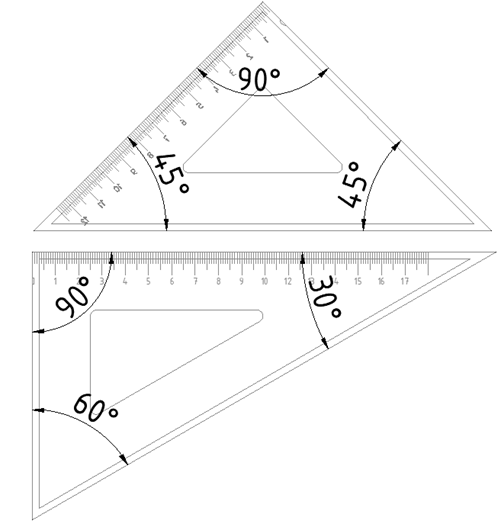
1. Dva trokuta (45-90-45) i (60 - 90 - 30),

2. Kutomjer

3. Ravnalo

4. Tehničku olovku 0.5

5. Gumicu za brisanje

Bez navedenog pribora učenik neće moći kvalitetno pratiti nastavu iz predmeta tehničko crtanje, stoga je vrlo važno redovno nošenje pribora. 

  • Uporaba pribora za crtanje u tehničkom crtanju

  • Crtanje okomitih i paralelnih pravaca

Crtanje okomitih i paralelnih pravaca izvodimo pomoću dva trokuta (jednakokračnog - pravokutnog i raznostraničnog - pravokutnog):

1. Crtanje okomitih pravaca

2. Crtanje paralelnih pravaca

 

  • Za domaći zadatak pomoću dva trokuta, kako je opisano na video uradcima, nacrtajte 5 paralelnih dužina čija je dužina 100 mm, a razmak između paralelnih pravaca 5 mm.
  • Za domaći zadatak pomoću dva trokuta, kako je opisano na video uradcima, nacrtajte 5 okomitih dužina čija je duljina 100 mm, a razmak između okomitih pravaca je 5 mm.
  • Mjerenje kutova kutomjerom

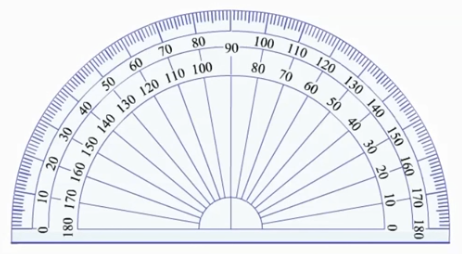
Mjerenje kutova čiji vrh leži u sjecištu dvaju pravaca, vrši se kutomjerom

1. Mjerenje kutova manjih od 180°

2. Mjerenje kutova većih od 180°

 

 

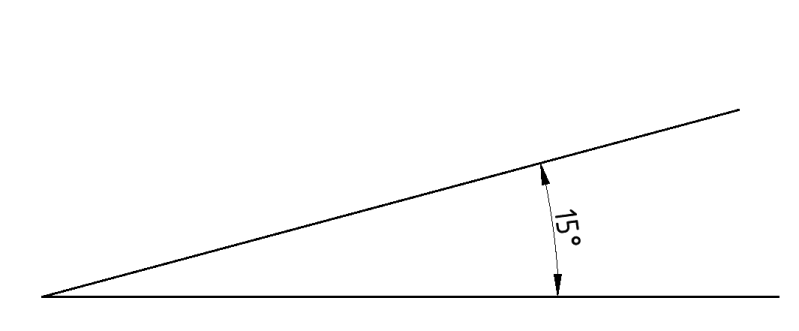
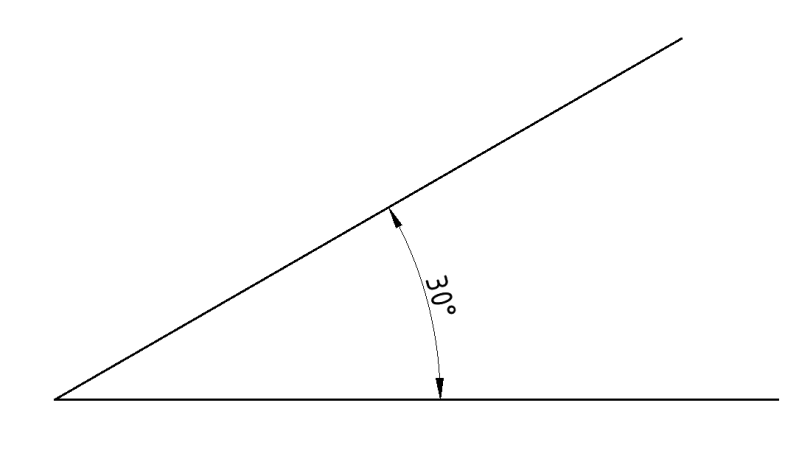
  • Za domaći zadatak pomoću kutomjera i pribora za crtanje, nacrtajte kutove: 15°, 30° i 47°.
  • Označite veličine kutova (kotirajte kutove), kako je prikazano na slikama a, b i c !

a.

b.

c.

  • Crtanje kutova 60°, 30°, 120°, 90°, 45° i 75°

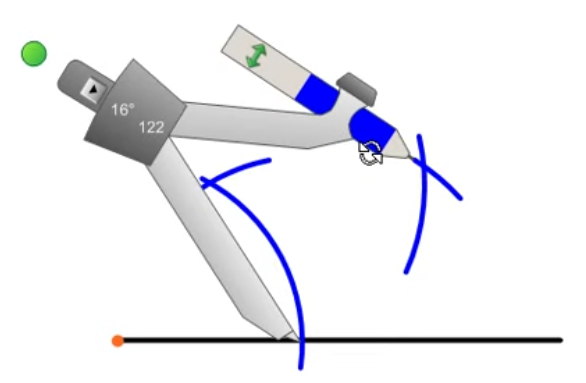
Crtanje kutova vršimo trokutom (ravnalom), šestarom i tehničkom olovkom. Točnost crtanja potrebno je provjeriti kutomjerom !

1. Crtanje kutova od: 60°, 30°, 120° i 90° ? 

2. Crtanje kutova od: 45° i  75°

  • Za domaći zadatak pomoću ravnala i šestara uredno u bilježnicu nacrtajte kutove: 60°, 30°, 120°, 90°, 45° i  75°.

  • Osnovna pravila u tehničkom crtanju

Osnovna pravila u tehničkom crtanju obuhvaćaju:

1. Širinu crta,

2.  Vrstu crta,

3.  Oblik tehničkog pisma,

4. Izgled i način kotiranja,

5. Formate papira,

6. Mjerila crtanja i

7. Zaglavlje crteža.

1. Širina crta u tehničkom crtanju

Širine crta se u tehničkom crtanju označavaju bojama, npr.:

○ 0,7 mm plavom

○ 0,5 mm smeđom

○ 0,35 mm žutom

○ 0,25 mm bijelom

Prema ISO sustavu na jednom papiru se primjenjuju tri širine crta, npr.:

(1)   0.7 mm, 0.5 mm i 0.35 mm

(2)   0.5 mm, 0.35 mm i 0.25 mm

(3)   0.35 mm, 0,25 mm i 0,18 mm

Na A4 formatu papira se najčešće crta tehničkom olovkom širinom crta 0,5 mm. Uz malu vježbu, lako se povlače crte uže crte 0.35 mm i još uže 0.25 mm.

U crtanju na računalu kada je predviđen ispis na formatu A4 lijepi rezultati se postižu skupinom crta 0.35 mm, 0.25 mm i 0.18 mm.

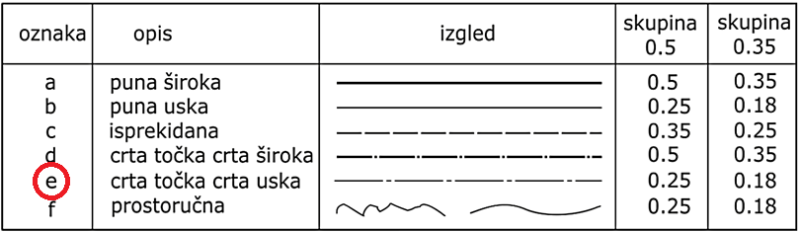
2. Vrsta crta u tehničkom crtanju

U tehničkom crtanju koriste se pet osnovnih vrsta crta:

Prijedlog za crtanje crta:

Namjena crta:

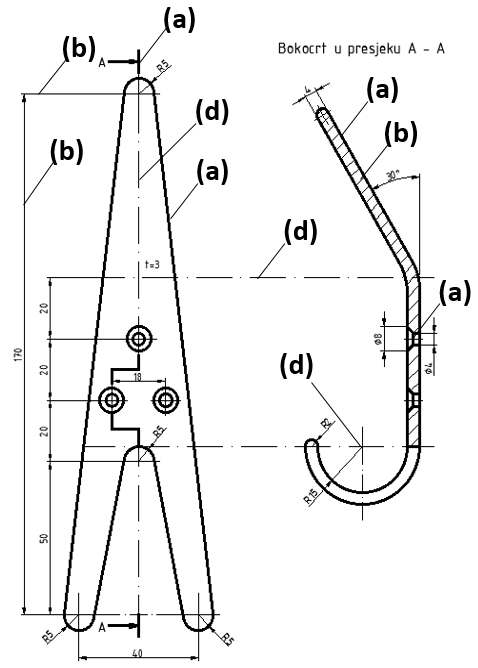
Primjer primjene crta u tehničkom crtanju, na radioničkog crteža vješalice:

Primjer primjene crta u tehničkom crtanju, na primjeru radioničkog crteža otvorenog ključa 13-17:

Primjer primjene crta u tehničkom crtanju, na primjeru radioničkog crteža otvorenog ključa za plin:

Primjer primjene crta u tehničkom crtanju, na primjeru radioničkog crteža vijka i matice s šesterokutnom glavom i metričkim navojem M30:

3. Oblik tehničkog pisma

Svaki tehničar treba znati tehnički crtež opisivati tehničkim pismom. Tehničko pismo može biti: široko, srednje ili usko, a može biti uspravno ili koso.

Osnovne karakteristike uspravnog tehničkog pisma srednje širine, visine 5 mm:

Oblik slova uspravnog tehničkog pisma srednje širine:

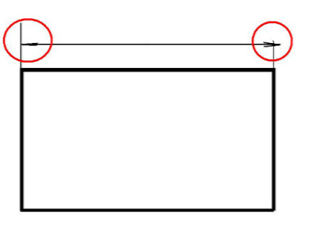
4. Izgled i način kotiranja

  • Elementi kota

Elementi kota su:

  • mjernice,
  • pomoćne mjerne crte,
  • strelice,
  • bridovi i
  • znakovi.

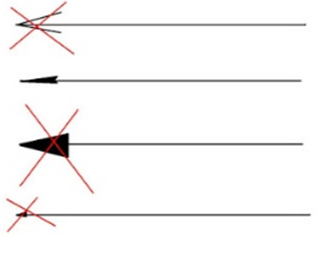
Izgled mjerne strelice:

  • Pravila nanošenja mjernih kota:
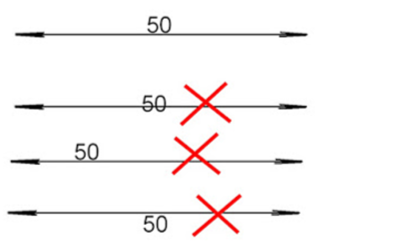
  1. svaka mjera na crtežu se kotira samo jednom;
  2. mjere u strojarstvu se predstavljaju u milimetrima, a jedinica mjere se ne piše;
  3. kotne linija se crtaju punom tankom linijom, a rubovi premeta punom debelom linijom;
  4. pomoćna kotna linija prelazi kotnu strelicu 1-2 mm;
  5. udaljenost prve kotne linije od ruba predmeta je 11 mm, a svake sljedeće paralelne kote 8 mm;
  6. kotni broj ne smije dodirivati kotnu liniju i uvijek se piše na sredini kotne linije;
  7. dužina kotne strelice je 3 mm;
  8. visina kotnog broje je 3 mm;
  9. kotni brojevi se pišu tehničkim pismom.

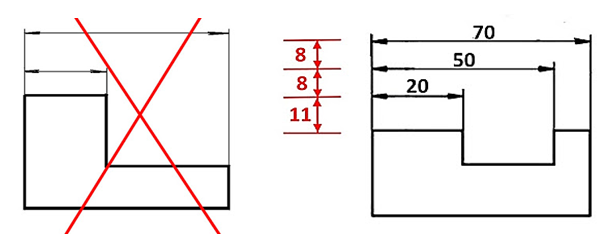
  • Greške prilikom kotiranja:

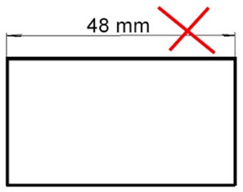
  • Dužina i oblik kotne strelice (strelica treba da bude uska i dužine približno3 mm)

 

 

  • Položaj kotnog broja (kotni broj iznad sredine kotne linije i ne smije da dodiruje kotnu liniju)

 

 

  • Jedinica mjere se ne piše pored kotnog broja.

  • Ako je riječ o strojarskom crtežu, podrazumijeva se da su mjere na kotama u milimetrima.

  • Ako je riječ o građevinskom arhitektonskom crtežu, podrazumijeva se da su mjere na kotama u centimetrima.

  • Ista dimenzija na predmetu se kotira samo jednom, može gore ili dolje, ali ne na oba mjesta !

  • Pomoćna kotna linija prelazi kotnu strelicu 1 – 2 mm (greška lijevo), a kotna strelica ne smije da prelazi pomoćnu kotnu liniju (greška desno).

  • Svi kotni brojevi na crtežu moraju biti iste visine (visina kotnog broja 3-4 mm),

  • Udaljenost prve kotne linije od ruba predmeta je 11 mm, a svake sljedeće je po 8 mm.

  • Na desnoj slici su prikazani zadovoljavajući razmaci između mjernica.

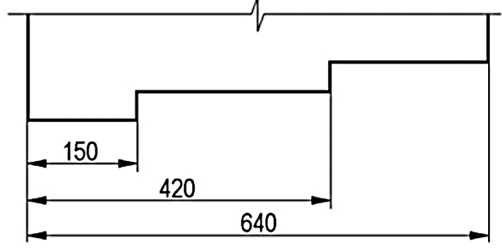
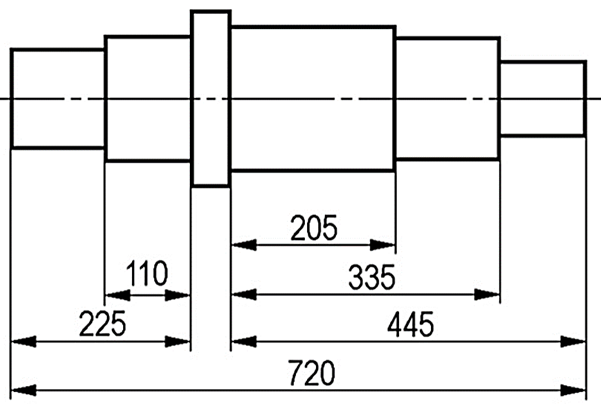
  • Ispravni primjeri i vrste kota:

Lančano kotiranje:

Paralelno kotiranje:

Kombinirano kotiranje:

Kotiranje tetive:

Kotiranje kružnog luka:

Kotiranje kuta:

Kotiranje duljine i polumjera i širine:

Linearno raspoređeni razmaci između provrta:

Kutno raspoređeni razmaci između provrta:

Kružno raspoređeni razmaci između provrta:

Kotiranje skošenih rubova:

Kotiranje skošenih rubova uz kut skošenja 45°:

Kotiranje upuštenih rubova provrta i rupa

5. Formati papira

Osnovni format papira za tehničko crtanje je A0. Prvi manji format je A1, a zatim A2, pa A3, A4, A5 ...

- Dimenzije formata A4 su 210 x 297 mm.

- Format A3 čine dva formata A4 pa ima dimenzije 420 x 297 mm.

- Format A2 čine dva formata A3 pa ima dimenzije 594 x 420 mm.

Slika prikazuje sve formate papira koje se koriste u tehničkom crtanju, najviše su u uporabi papiri A4, A3 i A2, tako da je potrebno zapamtiti njihove dimenzije:

6. Mjerilo crtanja

Ako se predmet ne može nacrtati u prirodnoj veličini, onda se crta umanjeno ili uvećano.

Dakle, mjerilom se neki objekt prikazuje uvećano ili umanjeno, ali pri tome predmet ne mjenja dimenzije. Bilo da je prednet na crtežu uvećan ili umanjen, na kote crteža upisujemo njegove stvarne dimenzije.

Primjer 1. Ako u prirodnoj veličini imamo kvadrat 25 x 25 mm, te ga želimo uvećati duplo na papiru u mjerilu M 2:1.

a) Kolika će biti stranica kvadrata na papiru u mjerilu M 2:1 ?

b) Koji mjerni broj ćemo upisati na mjernicu ?

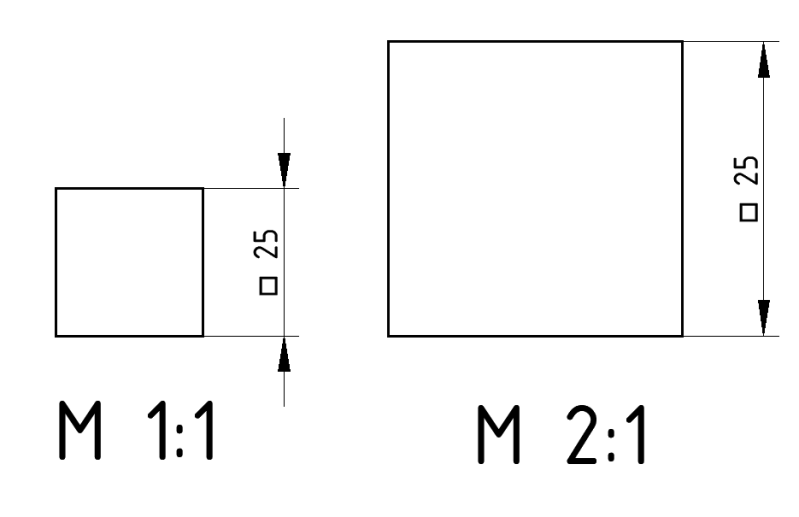
Odgovor:

a)Ako kvadrat želimo prikazati 2 x veći na papiru (M 2:1), tada ćemo sve stranice kvadrata pomnožiti sa 2, dakle crtamo   kvadrat 2∙25 mm = 50 mm

b) Na mjernicu ćemo upisati stvarnu duljinu 25, a ne uvećanu 50 !

Primjer 2. Slika prikazuje pravokutnik dimenzija a = 120 mm, b = 90 mm. U bilježnicu, pomoću pribora za crtanje nacrtajte isti pravokutnik ali u mjerilu M 1:3.

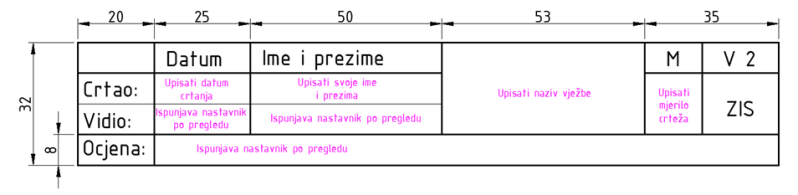
7. Zaglavlje crteža i okvir papira za crtanje

Svaki crtež ima okvir i sastavnicu. U sastavnicu se upisuju podatci o:

  • Crtežu: mjerilo, naziv crteža, broj crteža, šifra vježbe
  • Crtaču: ime i prezime, datumu crtanja
  • Pregledu crteža: datum, tko je pregledao i ocjena

Domaća zadaća:

Za domaću zadaću izradite na A4 formatu čistog papira, pomoću pribora za crtanje izradite okvir za crtanje i zaglavlje crteža koje u rubrikama sadržavati samo riječi: Crtao, Vidio, Ocjena, Datum, Ime i prezime, M.

  • Osnovne geometrijske konstrukcije

Osnovne geometrijske konstrukcije imaju osnovni zadatak da se savlada pravilnom načinu konstruiranja elementarnih geometrijskih konstrukcija, kao što su:

1. simetrale dužine i kutova,

2. konstrukcije kružnih lukova,

3. pravilnih višekuta,

4. kružnih prijelaza.

Sve navedene osnovne geometrijske konstrukcije kasnije će biti sastavni dio složenijih tehničkih crteža.

1.1. Simetrala dužine 

Simetrala dužine je pravac koji dužinu dijeli na dva jednaka djela.

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  1. Nacrtajte dužinu AB = 50 mm (tip linije a).

  2. Ubodite šestar u točku (B), te ga raširite tako da širina šestara bude malo dulja od polovice dužine AB.

  3. Povucite luk (L1) (tip linije - b).

  4. Ne mijenjajte širinu šestara ! Ubodite šestar u točku (A), i povucite luk (L2)

    (tip linije - b), koji će sjeći luk (L1), u dvije točke (T1) i (T2) kako je prikazano na slici lijevo.

  5. Nacrtajte pravac (tip linije - e), koji će proći kroz točke (T1) i (T2), pravac dijeli dužinu AB na dva jednaka dijela, što ga čini simetralom.

Video predavanje. TC - OGK - Vježba 1:

1.2. Simetrala kuta

Simetrala kuta je pravac koji dijeli kut točno na dva jednaka dijela.

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  1. Nacrtati zadani kut od 50°, koristeći kutomjer, označiti vrh (V), i krakove (a i b).

  2. Proizvoljno raširiti šestar i s njim povući luk koji sječe krakove a i b.

  3. Sjecište kraka (a) i luka, označiti sa (T1), a sjecište kraka (b) i luka slovom (T2).

  4. Raširite šestar proizvoljno i ubodite ga u točku (T1), te nacrtajte luk (L1), a zatim ne mijenjajte širinu šestara i ubodite šestar u točku (T2), i nacrtajte luk (L2), koji će sjeći luk (L1).

  5. Sjecište luka (L2) i (L1) označite slovom (T3).

  6. Povucite pravac tipa (e), koji prolazi kroz vrh trokuta (V) i točku(T3). Ovaj pravac jest simetrala kuta i dijeli kut na dva jednaka dijela 50° : 2 = 25°. Izmjerite nacrtanu polovinu kuta, kako biste se uvjerili da ste točno konstruirali simetralu.

Video predavanje. TC - OGK - Vježba 2.

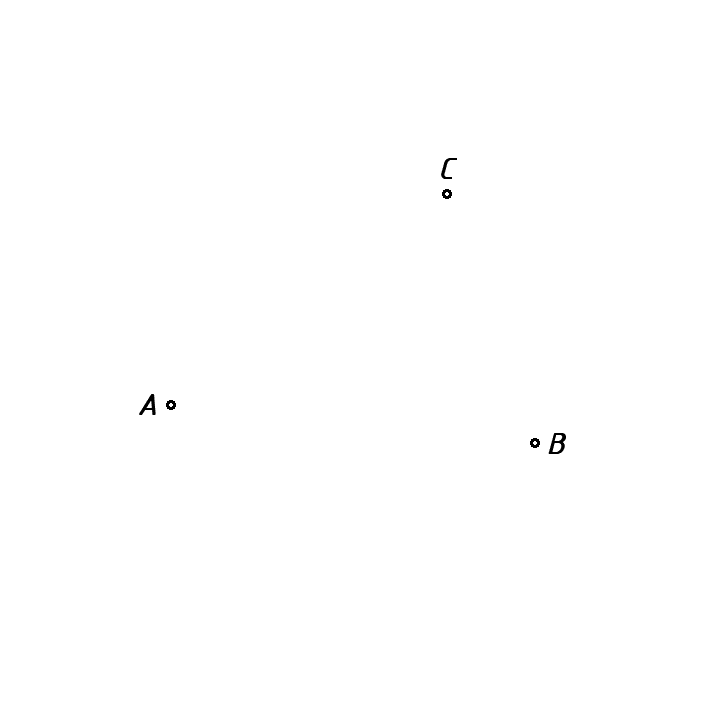
1.3. Konstrukcija kružnice kroz tri zadane točke

Slika a)

Slika b)

Slika c)

Slika d)

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

a) Proizvoljno nacrtati tri točke na papiru (približno kao na slici a), te ih obilježiti slovima A, B i C.

b) Spojiti točke tako da dobijemo dvije dužine, dužinu AB i dužinu BC (slika b).

c) Pronaći simetralu dužine AB i simetralu dužine BC. Sjecište dvaju simetrala daje točku T.

d) Šestar ubosti u točku T, raširiti ga do točke A (do točke A, B ili C), i nacrtati kružnicu.

Video predavanje. TC-OGK-Vježba 3:

1.4. Spajanje pravaca pomoću kružnih lukova

Dva pravca koja se nalaze pod određenim kutom, potrebno je spojiti konkavnim ili konveksnim lukom u odnosu na pravce koje spajaju.

Poznavanje izrade kružnih prijelaza, nužno je za kvalitetnu izradu radioničkih crteža.

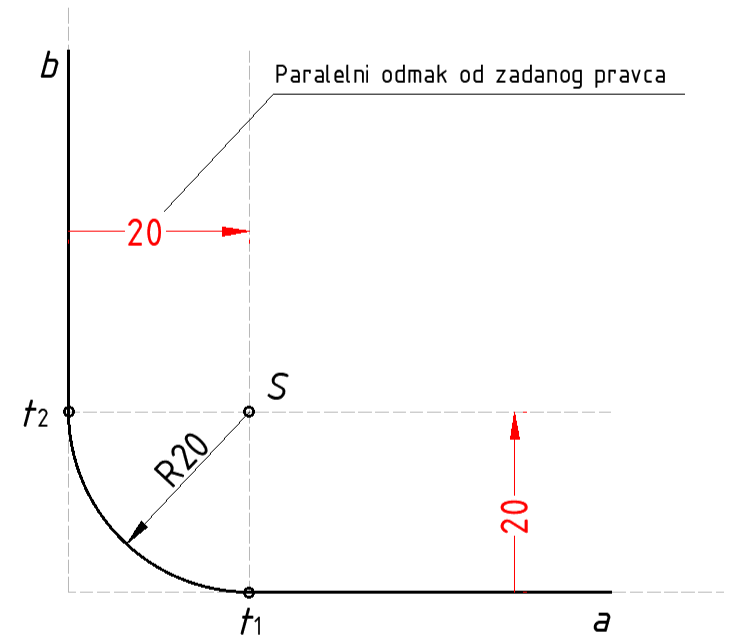
Primjer 1. Prikazana dva pravca spojite konveksnim lukom R20.

Slika a)

Zadano

Slika b)

Traži se

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  1. Na slici a) su zadana dva pravca (a i b).

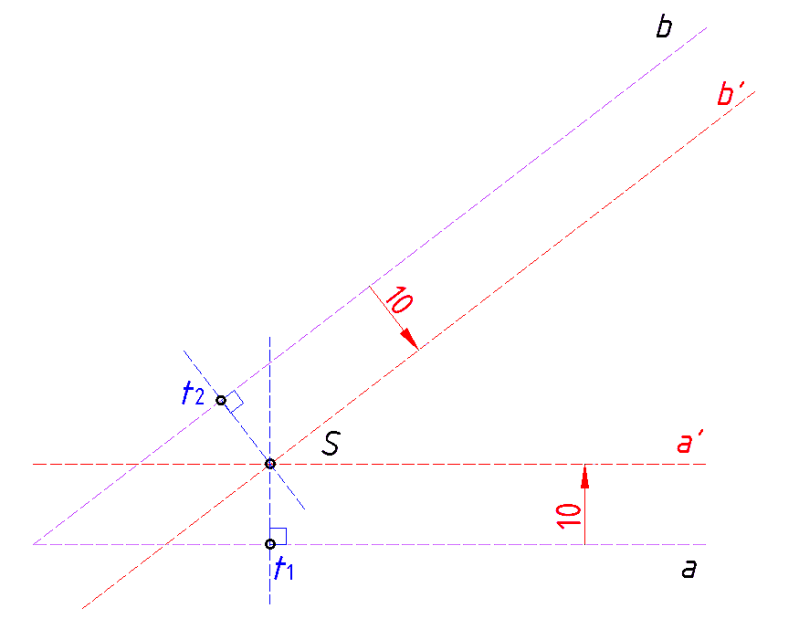
  2. Nacrtajte pravac b', koji je paralelan pravcu b i od pravca b, odmaknut za veličinu radijusa, konveksnog luka (R20), tj. 20 mm. Isto napraviti i sa pravcima a' i a.

  3. Sjecište pravaca a' i b', označite točkom S, sjecište pravaca a i a' označite oznakom (t1), a sjecište pravaca b i b', označite točkom (t2).

  4. Ubodite šestar u točku S, raširite ga do točke  (t1) i konstruirajte luk do točke (t2). 

  5. Konstruirali ste sada konveksan luk radijusa R20 mm koji spaja dva pravca, još je samo ostalo da podebljate pravce a i b, kako prikazuje slika b).

Primjer 2. Prikazana dva pravca spojite konveksnim lukom R10.

Slika a) Zadano

Slika b) Postupak

Slika c) Traži se

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  1. Na slici a) su zadana dva pravca (a i b).

  2. Nacrtajte pravac b', koji je paralelan pravcu b i od pravca b, odmaknut za veličinu radijusa, konveksnog luka (R10), tj. 10 mm. Isto napraviti i za pravcima a' i a.

  3. Sjecište pravaca a' i b', označite točkom S.

  4. Na pravac a povucite okomicu, koja prolazi kroz točku S. Na pravac b povucite okomicu koja prolazi kroz točku S.

  5. Sjecište okomice i pravca a označite oznakom (t1), a sjecište druge okomice i pravca b označite oznakom (t2).

  6. Podebljajte (tipom linije a), pravac a od točke (t1), do kraja pravca. Također podebljajte pravac b, od točke (t2), do kraja pravca.

  7. Ubodite šesta u točku S i raširite ga do točke (t1), i šestarom nacrtajte kružni luk od toče (t1) do točke (t2).

  8. Konstruirali ste sada konveksan luk radijusa R10 mm koji spaja dva pravca, podebljate pravce a i b, kako prikazuje slika c).

  9. Obrišite sve pomoćne linije koje ste koristili da konstruirate obli prijelaz, kako prikazuje slika c).

Video predavanje. TC-OGK-Vježba 4.1:

Video predavanje. TC-OGK-Vježba 4.2:

1.5. Spajanje pravca s lukom, kružnim prijelazom

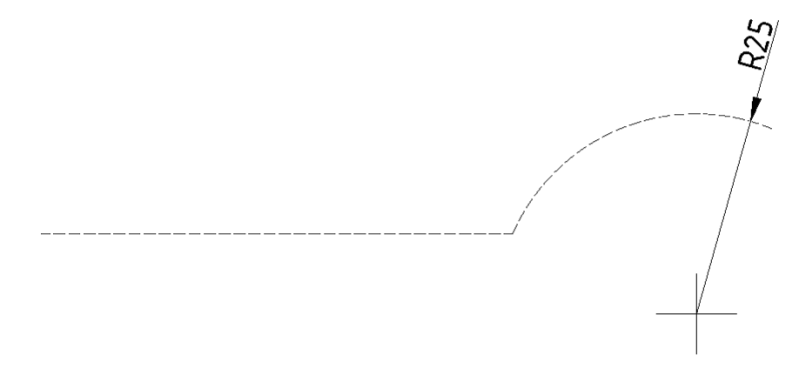
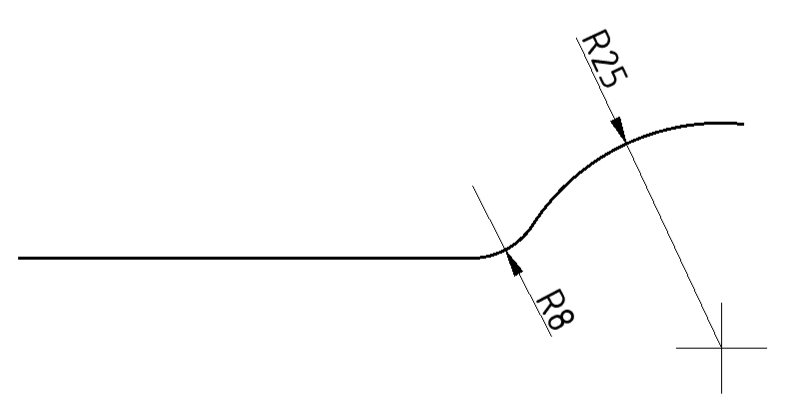
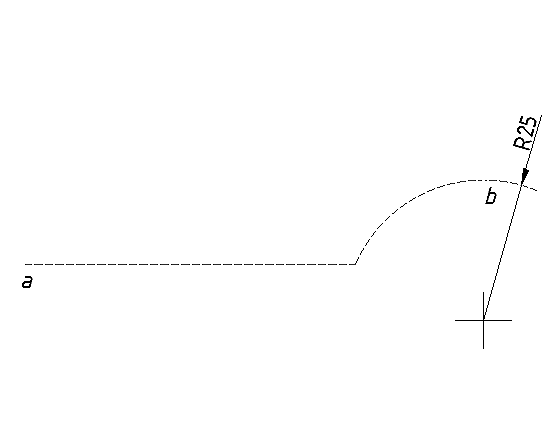
Slika a) prikazuje spoj luka čiji je polumjer 25 mm (R25) i pravca. Luk i pravac potrebno je spojiti kružnim prelazom polumjera 8 mm (R8), kao na slici b).

Slika a) Zadano

Slika b) Traži se

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

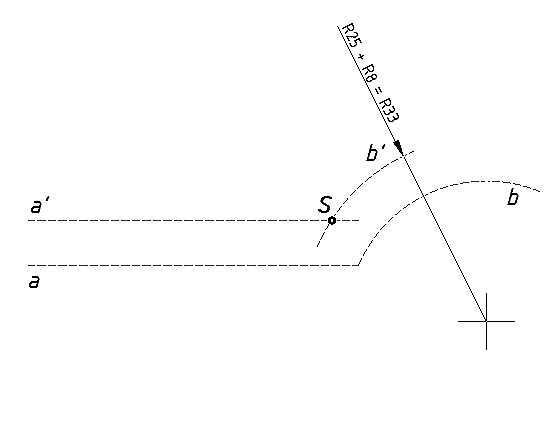
Slika prikazuje pravac a i luk b, koji moramo spojiti oblim prelazom (kružnim lukom R8)

Pravcu a, povući paralelan pravac a', udaljen od pravca a za 8 mm (veličina radijusa zaobljenja)

Pravac a' treba presjeći lukom b' čiji je radijus veličine R25 + R8 = R33, i označiti sjecište točkom S.

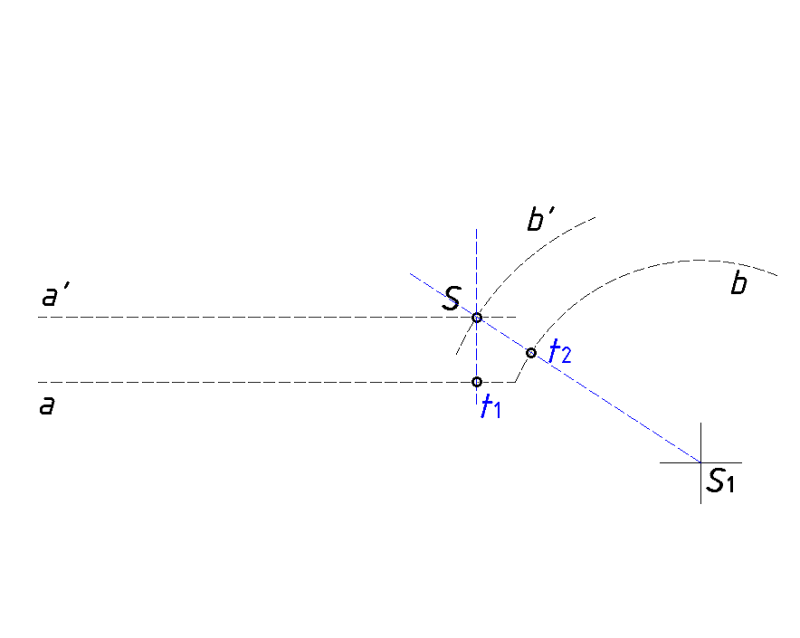
Povući okomicu na pravac a' tako da ta okomica prolazi kroz točku S, a sjecište okomice i pravca označiti kao točku (t1). 

Povući pravac koji prolazi kroz točku S i točku (S1) ishodište luka R25 mm.

Sjecište pravca koji spaja te dvije točke označiti točkom (t2).

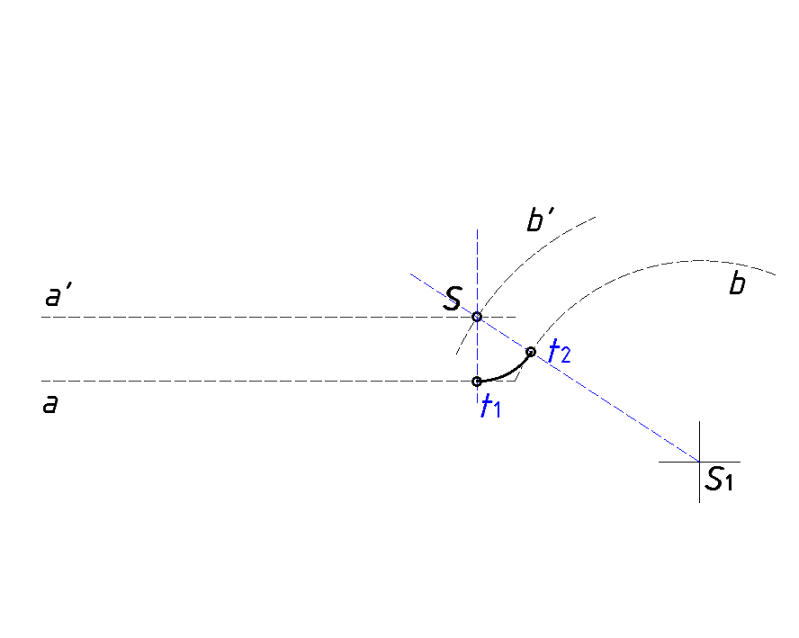
Ubosti šestar u točku S, raširiti ga to točke (t1) i povući luk do točke (t2).

Podebljati pravac a i luk b do točaka (t1) i (t2).

Podebljati mjesta prelaza kod točaka (t1) i (t2), tako da izgledaju što je glađe moguće te prijelazi u tim točkama budu što manje uočljivi (kao na slici lijevo).

Obrisati sve pomoćne pravce, i kotirati lukove.

Video predavanje. TC-OGK-Vježba 5:

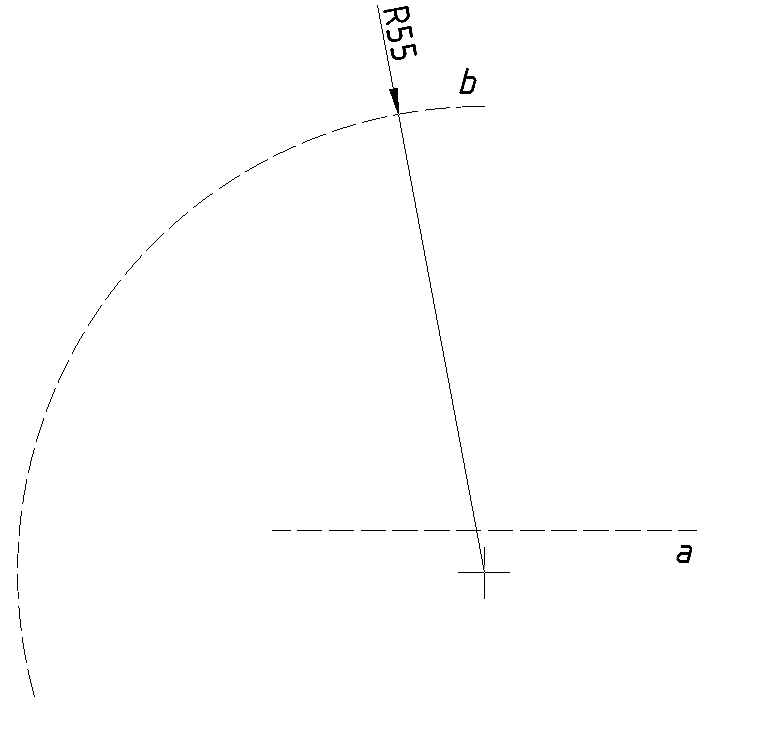
1.6. Spajanje luka i pravca konveksnim lukom 

Zadatak je spojiti pravac a s lukom b, radijusa R55 mm. Luk i pravac spojite konveksnim lukom radijusa R10 mm.

Zadano:

Traži se:

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

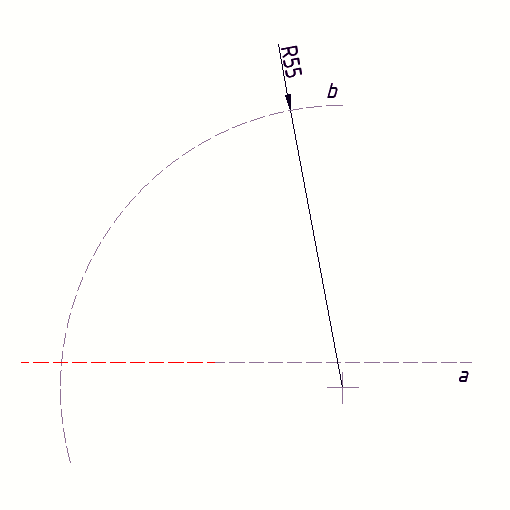
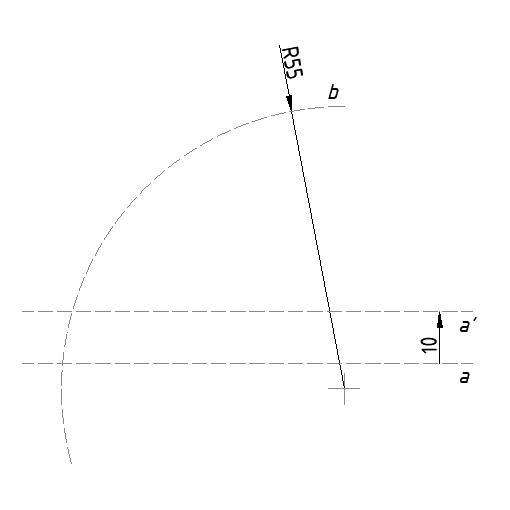
  • Od nas se traži da spojimo pravac a s lukom b konveksnim lukom radijusom R10 mm.
  • Produžiti pravac a, tako da sječe luk b.
  • Povući pravac a' koji će biti paralelan pravcu a i od njega udaljen 10 mm (jer je zadani polumjer konveksnog luka R10 mm)
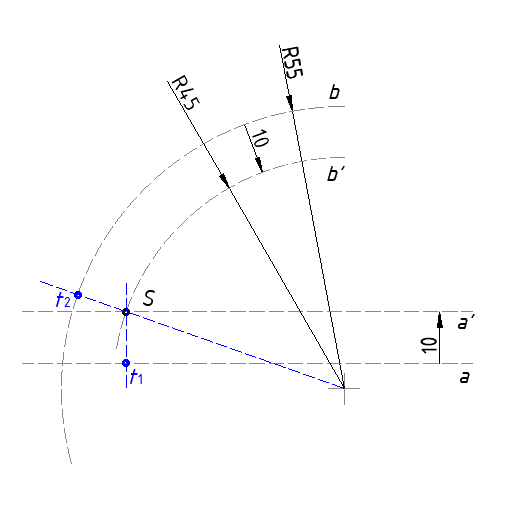
  • Raširiti šestar na duljinu 45 mm ( R55-R10 =R45 mm), ubosti ga u ishodište luka b i konstruirati novi luk b' koji će sjeći pravac a'. Sjecište luka b' i pravca a' označite točkom S.
  • Točka S će biti ishodište konveksnog luka koji spaja luk b i pravac a. Sada je potrebno utvrditi gdje konveksni spojni luk R10 počinje (t1) i gdje završava (t1).

 

  • Povući okomicu na pravac a koja prolazi kroz točku S, sjecište okomice i pravca a označiti točkom (t1) (to je početna točka konveksnog luka).
  • Konstruirati pravac, koji će početi u ishodištu luka a, i povući ga kroz točku S tako da sječe luk b.  Sjecište pravca i luka b označiti točkom (t2) (to je krajnja točka konveksnog luka).
  • Izbrisati sve pomoćne linije i lukove koje ste prethodno nacrtali, kako slika prikazuje.
  • Ubosti šestar u točku S.
  • Raširiti šestar do točke (t1).
  • Nacrtati konveksni kružni luk punom širokom crtom (tip a) koji završava u točki (t2).
  • Podebljati pravac a.
  • Podebljati luk b (R55).
  • Kotirati kružne lukove prema pravilima tehničkog crtanja, paziti na debljinu mjernica puna uska linija (linija tip b), paziti na izgled strelice i paziti na izgled mjernih brojeva (pisati ih tehničkim pismom).

Video predavanje. TC-OGK-Vježba 6:

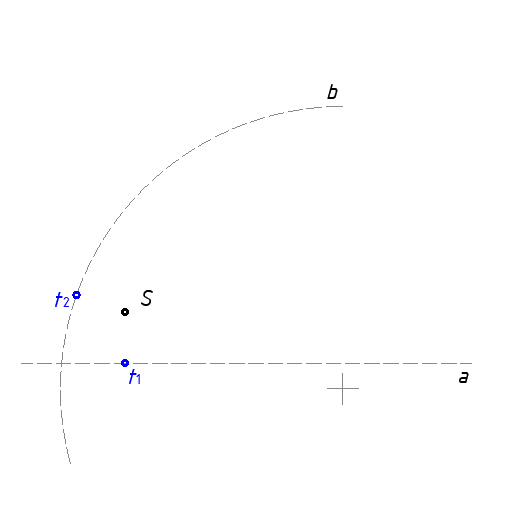
1.7. Spajanje dva luka s konveksnim lukom 

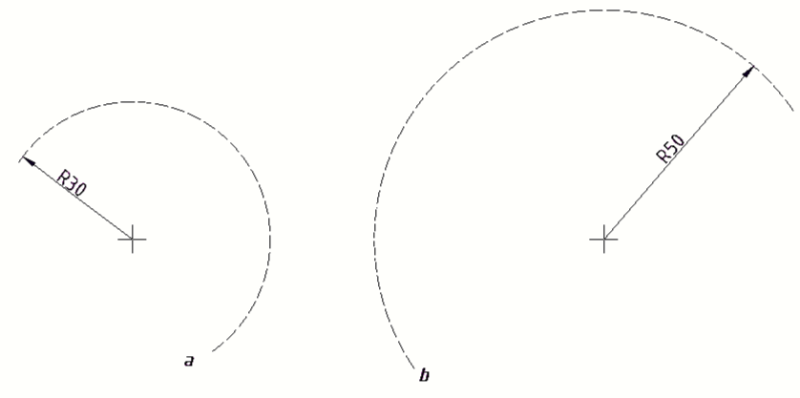
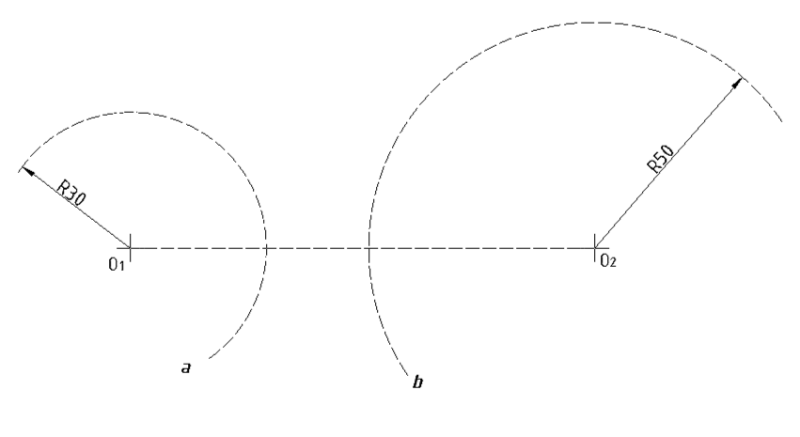
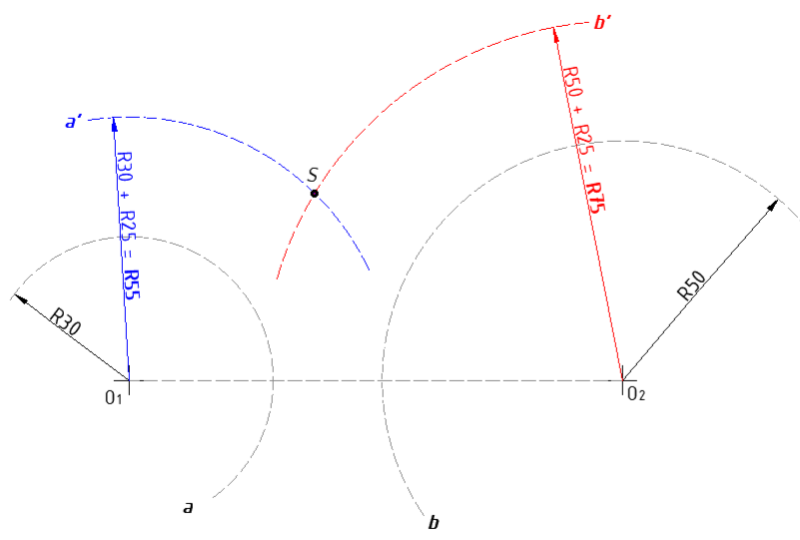
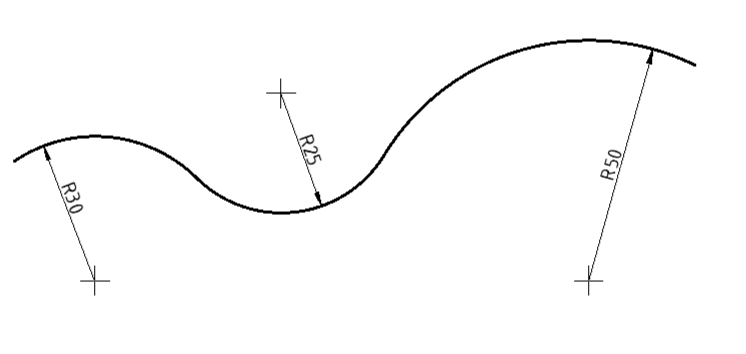
Zadani su luk a (R30) i luk b (R50). Spoji luk a i b spoji konveksnim lukom radijusa R25 mm.

Zadano:

Traži se:

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  • Spojiti ishodišta dvaju lukova nevidljivom linijom.
  • Radijus luka kojim spajamo zadane lukove je duljine 25 mm ! Ovom luku moramo naći ishodište S. Ovo ćemo napraviti konstrukcijom lukova a' i b'.
  • Luk a' ima radijus veličine R30 + R25 = R55 mm.

- Šestar raširiti na 55 mm, zabosti ga u  O1 i povući luk a', kako prikazuje slika.

  • Luk b' ima radijus veličine R50 + R25 = R75 mm.

- Šestar raširiti na 75 mm, zabosti ga u  O2 i povući luk b', kako prikazuje slika.

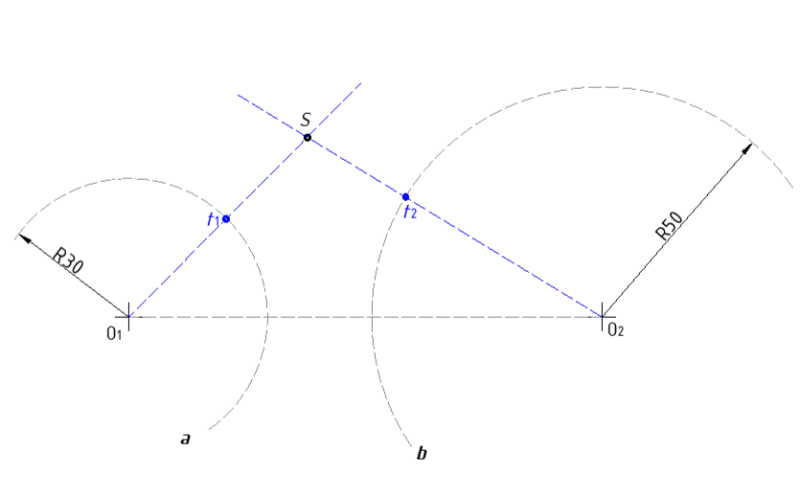
  • Sjecište luka a' i luka b', daje točku S koja je ishodište konveksnog luka koji spaja luk a i b. Označiti točku S !
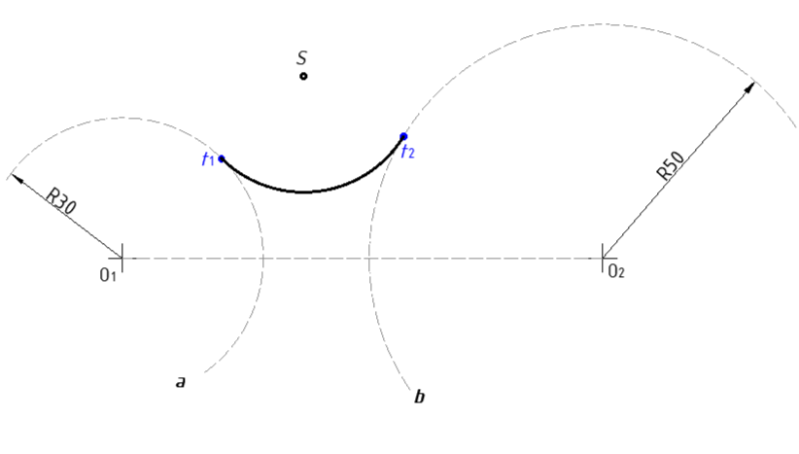
  • Sjecište pravca koji prolazi kroz točku O1 i točku S, jest točka t1. Točka t1 je točka u kojoj počima konveksni luk, koji spaja dva zadana luka.
  • Sjecište pravca koji prolazi kroz točku O2 i točku S, jest točka t2. Točka t2 je točka u kojoj završava konveksni luk, koji spaja dva zadana luka.
  • Crtanje konveksnog spojnog luka:
  • Ubosti šestar u točku S, raširiti ga do točke t1. i povući punom širokom linijom luk do točke t2.
  • Podebljati lukove R30 i R50, i voditi računa da se sva tri luka poklapaju !
  • Obrisati sve prethodno nacrtane "nevidljive" tanke linije, označiti ishodišta lukova križićima te kotirati radijuse lukova prema pravilima tehničkog crtanja.

Video predavanje. TC-OGK-Vježba 7:

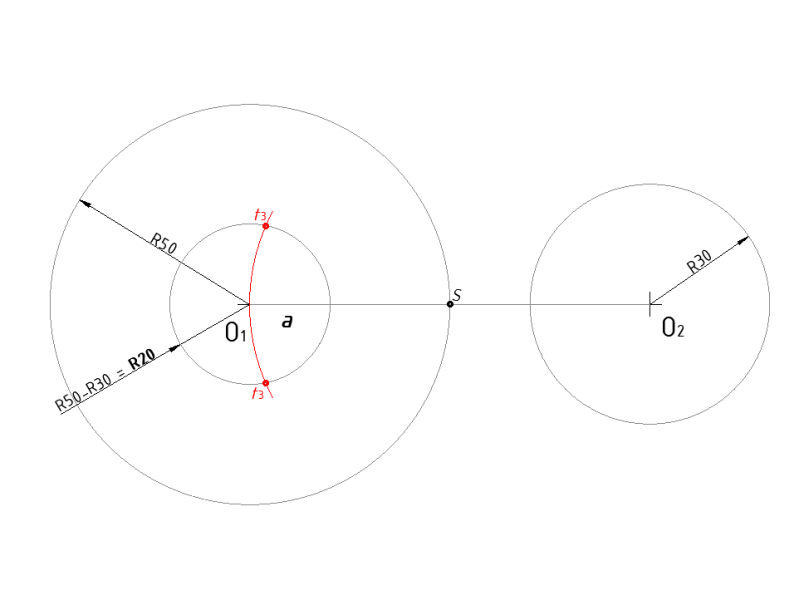
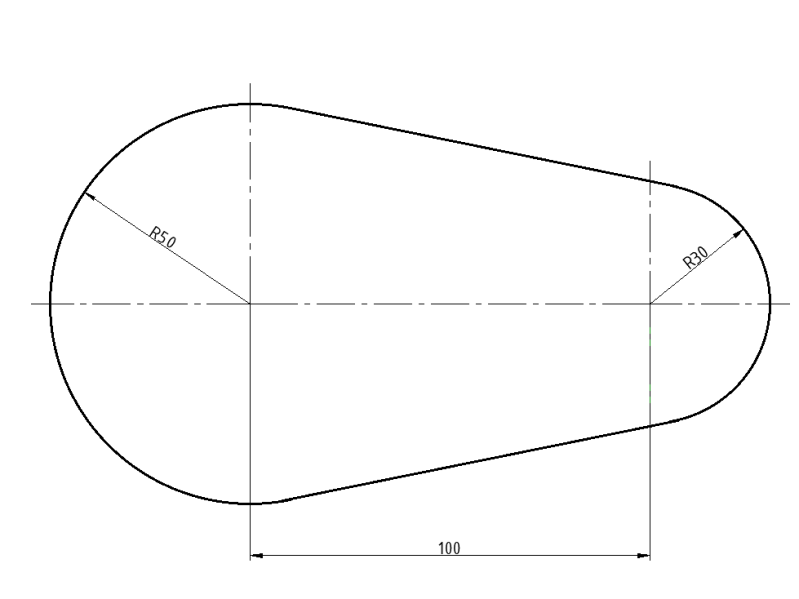
1.8. Spajanje kružnica tangentama

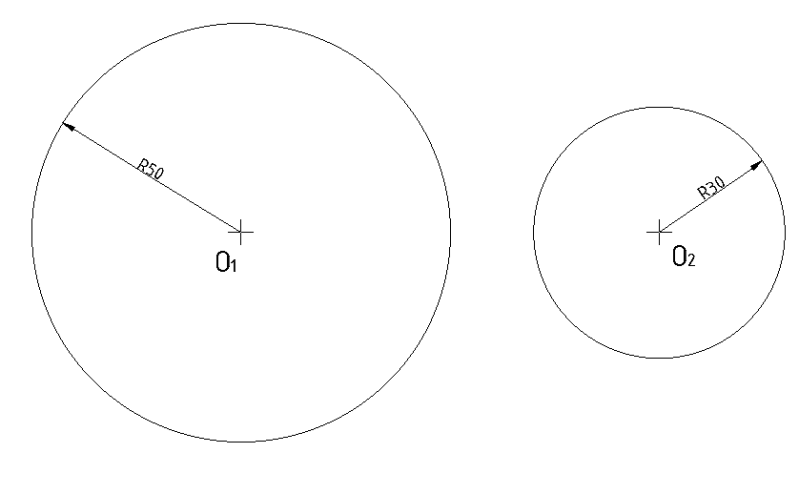
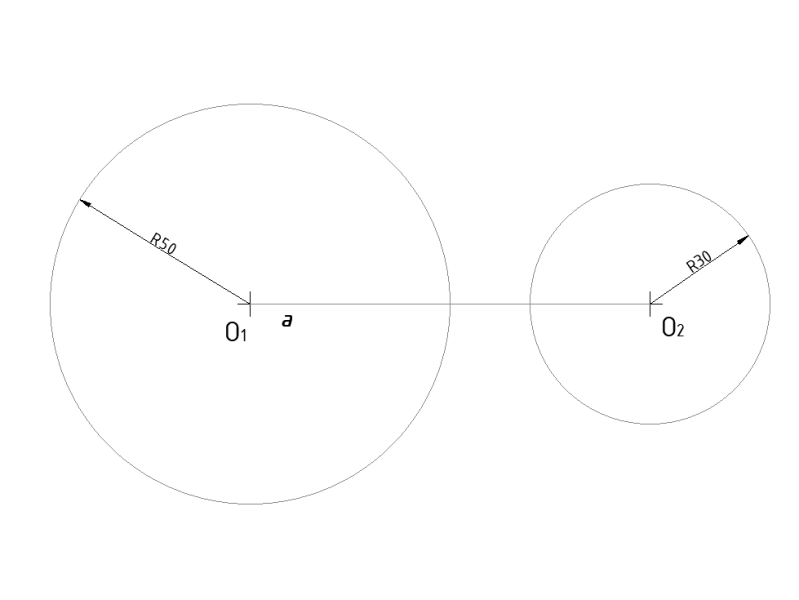
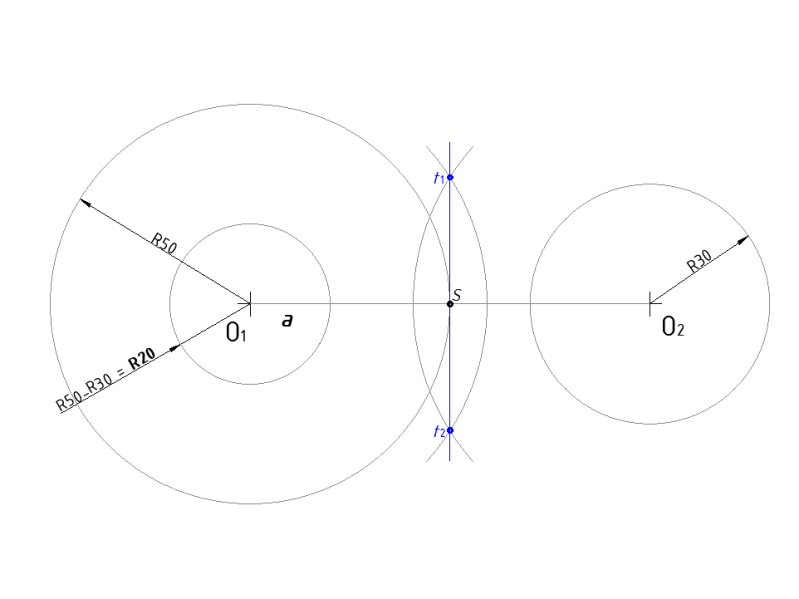
Zadane je kružnica O1 čiji je radijus R50 mm i kružnica O2 čiji je radijus R30 mm. Potrebno je dvije kružnice spojiti tangentnim pravcima*. 

*Tangentni pravac je pravac koji kružnicu dodiruje (tangira), samo u jednoj točki.

Zadano je:

Traži se:

Postupak crtanja:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

  • Spojiti pravcem a ishodišta zadanih kružnica (O1 i O2).
  • Pronađi simetralu dužine O1O2. Da se prisjetiš kako se crta simetrala dužine, ponovi lekciju 1.1. Simetrala dužine.
  • Konstruiraj kružnicu radijusa R50-R30 = R20 mm, s ishodište u točki O1.
  • Sjecište simetrale koja prolazi kroz točke t1  i t2 i pravca a , označite točkom S.
  • U točku S  ubosti šestar i raširiti ga do točke  O1
  • Nacrtati luk koji će sjeći kružnicu R20 mm u točkama t3 i  t4.
  • Iz ishodišta kružnice (O1), povući pravac koji će prolaziti kroz točku t3 i  sjeći kružnicu R50 u točki t5.
  • Iz ishodišta kružnice (O1), povući pravac koji će prolaziti kroz točku t4 i  sjeći kružnicu R50 u točki t5.
  • Pravac koji prolazi kroz točke (O1,t3 ,t5), prenijeti paralelno uz pomoć dva trokuta u ishodište kružnice O2.
  • Pravac koji prolazi kroz točke (O1,t4 ,t6), prenijeti paralelno uz pomoć dva trokuta u ishodište kružnice O2.
  • Pravci sijeku kružnicu (O2) u točkama (t7 ,t8).
  • Sve nepotrebne, pomoćne nevidljive linije izbrisati !
  • Spojiti točke t5 ,t7 i t6 ,t8.
  • Obrišite točke t5 ,t7 i t6 ,t8.
  • Podebljajte konture crteža punom širokom linijom tip-a, nacrtajte simetrale lukova linijom tip-d, te kotirajte radijuse kružnica, prema pravilima kotiranja u tehničkom crtanju, kotirajte razmak između kružnica također prema pravilima kotiranja u tehničkom crtanju.

Video predavanje. TC-OGK-Vježba 8:

1. Dio:

2. Dio:

  • Konstrukcije pravilnih mnogokuta

U monogokute ubrajamo sve geometrijske likove koji imaju više od dva kuta. Da bismo geometrijski lik s više od dva kuta nazvali pravilnim, veličine svih kutova moraju biti jednake.

1.1. Konstrukcija trokuta

U ovoj nastavnoj jedinici, prisjetit ćemo se kako se crtaju najjednostavniji mnogokuti, tj. kako se crtaju različiti trokuti; jednakostranični, jednakokračni, raznostranični i pravokutni.

a) jednakostranični trokut

  • jednake duljine stranice
  • jednake veličine kutova
  • zbroj kutova 180°

b) jednakokračni trokut

  • dvije stranice jednakih duljina
  • dva kuta jednake veličine
  • zbroj kutova 180°

c) raznostranični trokut

  • sve stranice različitih duljina
  • svi kutovi različitih veličina
  • zbroj kutova 180°

d) pravokutni trokut

  • stranice različitih duljina
  • različite veličine kutova
  • zbroj kutova 180°

Valja zapamtiti:

  • jednakostranični trokut ima sve stranice jednakih duljina, i sva tri kuta jednake veličine,

  • jednakokračni trokut ima dvije stanice jednake duljine, i dva kuta jednake veličine,

  • raznostranični trokut, nema niti jednu stranicu jednake duljine, a samim time on ima tri kuta različite veličine,

  • pravokutni trokut, može biti; jednakokračan-pravokutni, raznostranično-pravokutan, ali uvijek ima jedan kut pravi, to je kut koji ima 90°.

Konstrukcija jednakostraničnog trokuta:

TC OGK V 9.1.

Konstrukcija jednakokračnog trokuta:

TC OGK V 9.2.

Konstrukcija raznostraničnog trokuta:

TC OGK V 9.3.

Konstrukcija pravokutnog trokuta:

TC OGK V 9.4.

1.2. Konstrukcija pravilnih četverokuta

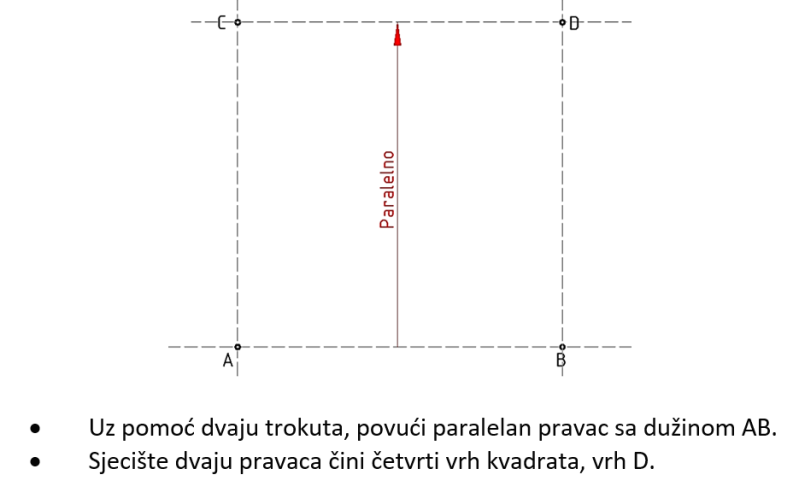
U ovoj nastavnoj jedinici prisjetit ćete se gradiva iz osnovne škole, te ćete ako ste zaboravili naučiti kako konstruirati kvadrat i pravokutnik. Kvadrat i pravokutnik su dva mnogokuta kojima je zajedničko to što imaju po četiri prava kuta. Kvadrat za razliku od pravokutnika ima sve stranice jednake duljine.

1.2.1. Konstrukcija kvadrata

Konstruirajmo kvadrat čija je duljina stranice a = 70 mm.

1.2.2. Konstrukcija pravokutnika

Konstruirajmo pravokutnik čije su stranice duljine a = 70 mm, b = 50 mm.

Postupak crtanja kvadrata:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

▶ Potrebno je konstruirati kvadrat čija je stranica duljine a = 70 mm.

Postupak crtanja pravokutnika:

Savjet: sve linije crtajte tankom "nevidljivom" linijom, kako biste mogli lakše ispravljati pogreške, a na kraju podebljajte ovisno o vrsti linije i potrebnoj širini linije.

▶ Potrebno je konstruirati pravokutnik čije su stranice duljine a=70 mm i b = 50 mm.

Konstrukcija kvadrata i pravokutnika

TC OGK V 10.1 - kvadrat:

TC OGK V 10.2 - pravokutnik:

1.3. Konstrukcija pravilnih peterokuta

1.4. Konstrukcija pravilnih šesterokuta

1.5. Konstrukcija pravilnih osmerokuta

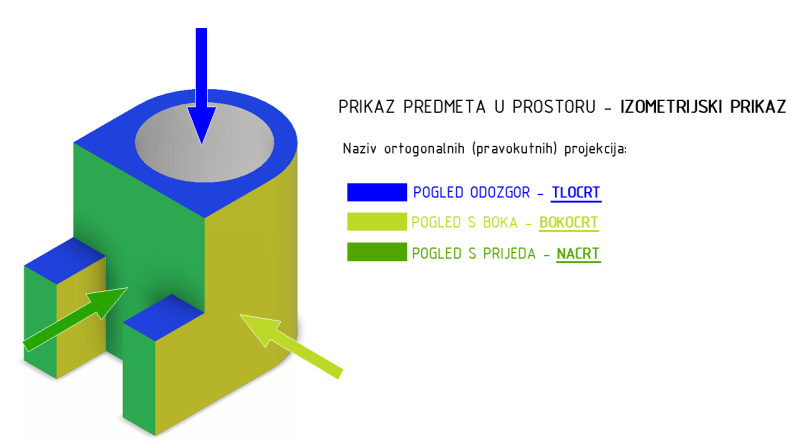
  • Pravokutno projiciranje

Pravokutne projekcije zadanog predmeta:

Skripta:

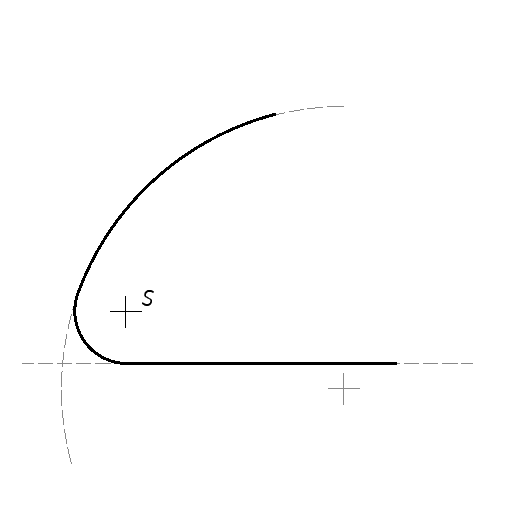
Create Your Own Website With Webador